94. Binary Tree Inorder Traversal

题目描述：

給定一個二元樹的根節點 root，返回它的中序遍歷(inorder traversal)結果。

解題思路:
二元樹（Binary Tree）總共有三種深度優先（DFS）遍歷方式，包括前序遍歷（preorder traversal）、中序遍歷（inorder traversal）和後序遍歷（postorder traversal），我們可以結合圖解來說明:

1. 前序遍歷（preorder traversal）：在節點的左邊劃一條線，表示優先訪問根節點，然後依次訪問左子樹和右子樹。
2. 中序遍歷（inorder traversal）：在節點的下方劃一條線，表示先訪問左子樹，再訪問根節點，最後訪問右子樹。
3. 後序遍歷（postorder traversal）：在節點的右邊劃一條線，表示先訪問左子樹，再訪問右子樹，最後訪問根節點。

然後，我們可以想像從樹的左邊開始，沿著整個樹的輪廓移動。在這個過程中，每次接觸到劃出的線條，就表示遍歷到該節點。這樣，通過手動的方式就能夠模擬出二元樹的遍歷順序。

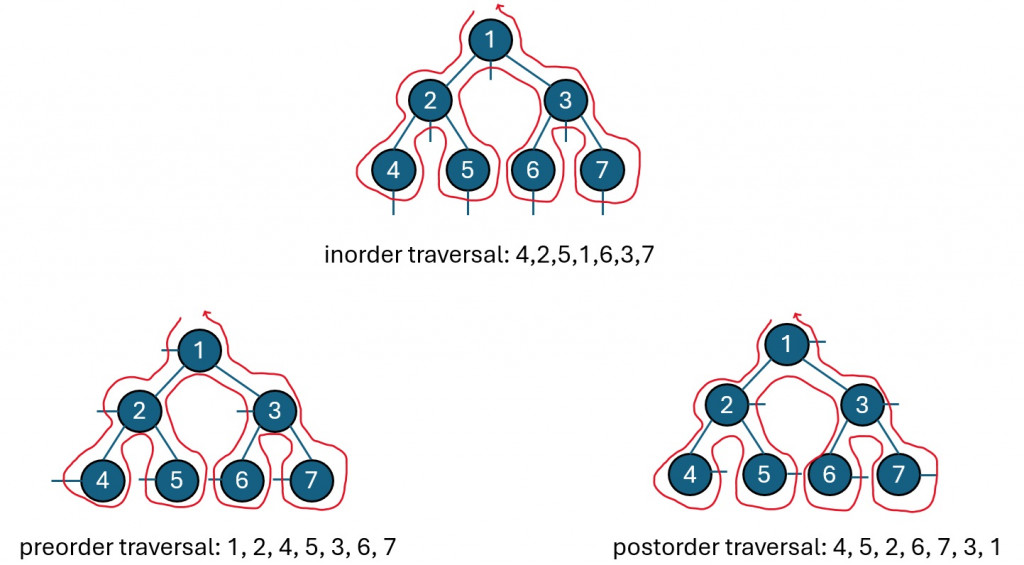
談論到二元樹的遍歷實作方式時，通常會有兩種方法：遞迴（recursion）和迭代（iteration）。

遞迴（recursion） 是最直觀的解法。遞迴的邏輯非常符合樹的結構本身，因為樹的每個子樹也是一棵樹，因此我們可以直接利用遞迴來實現遍歷。以中序遍歷為例，遞迴的實作方式如下：

1. 遞迴遍歷左子樹：首先，對當前節點的左子樹進行遞迴遍歷。
2. 訪問根節點：在完成左子樹的遍歷後，訪問根節點（即當前節點）。
3. 遞迴遍歷右子樹：最後，對當前節點的右子樹進行遞迴遍歷。
   

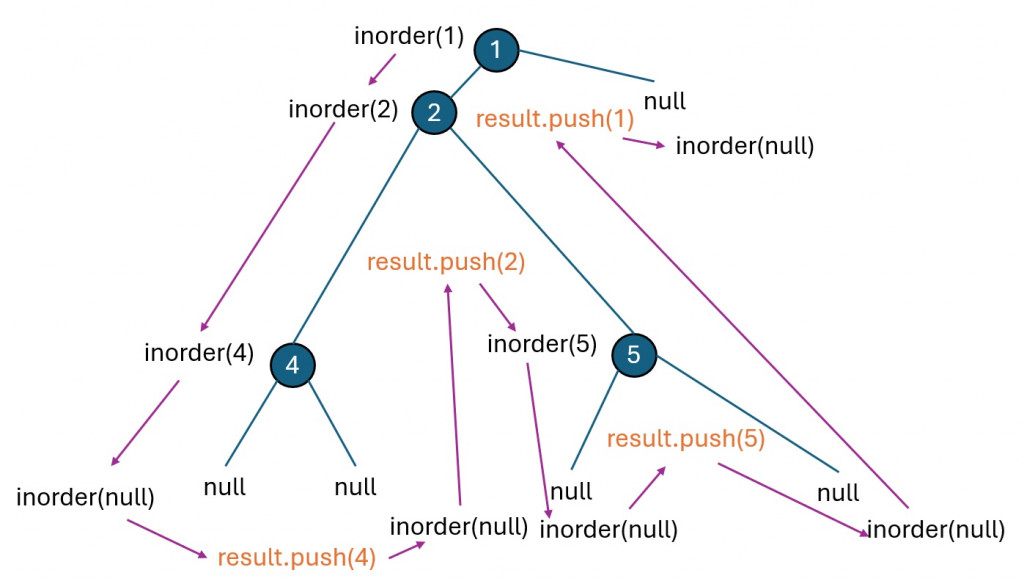
var inorderTraversal = function(root) {
    const result = [];

    function inorder(node) {
        if (node == null) return;

        inorder(node.left);
        result.push(node.val);
        inorder(node.right);
    };

    inorder(root);

    return result;
};

時間複雜度：O(n)，需要遍歷所有節點。
空間複雜度：O(h)，其中 h 是樹的高度，遞迴調用call stack的空間取決於樹的高度。

相比遞迴，迭代（iteration）實作過程相對複雜許多，需要使用stack來模擬遞迴過程。具體來說，我們會將所有左子節點依次push到stack，直到遇到葉子節點後開始從stack中pop出來並訪問節點，然後再處理右子樹。

迭代的過程可以描述如下：

1. 初始化一個空的 stack：這個 stack 用來保存需要處理的節點。
2. 將所有左子節點push到stack：從根節點開始，將當前節點和所有左子節點依次push到stack，直到到達最左端的節點（即葉子節點）。
3. 開始從stack中pop出來並訪問節點：當到達最左端的節點後，開始從stack中pop出來並訪問節點，然後移動到右子樹進行處理。
4. 重複步驟 2 和 3：重複這個過程直到所有節點都被訪問完畢。
   這個過程可以理解為模擬遞迴中的「左 -> 根 -> 右」的順序，不過這裡是手動控制訪問順序，而不是由系統的調用call stack自動處理。
   

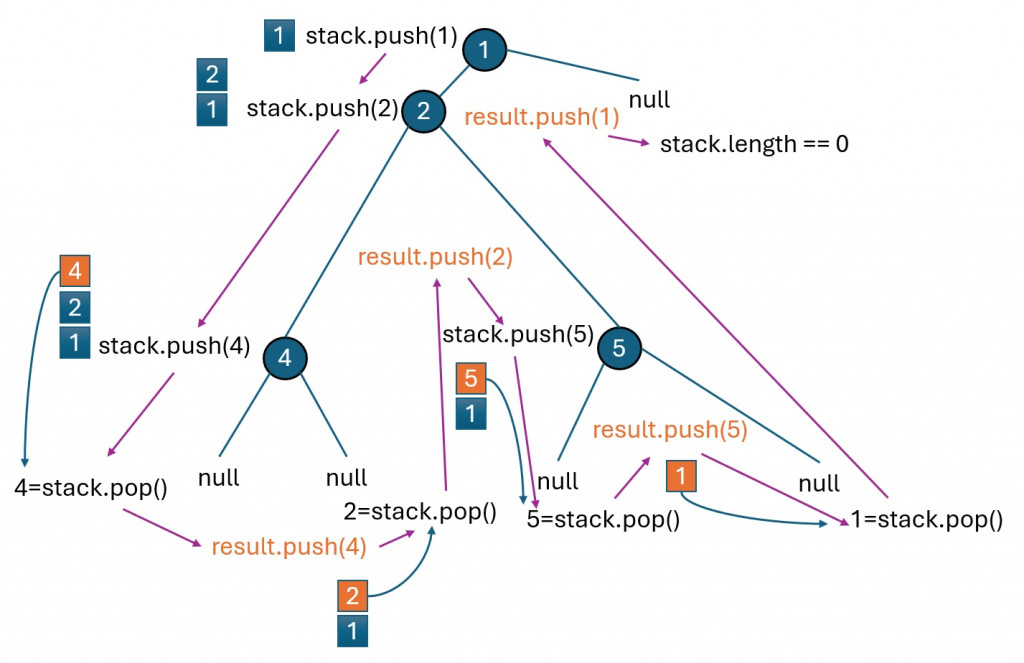
var inorderTraversal = function(root) {
    const result = [];
    const stack = [];
    let current = root;

    while (current !== null || stack.length > 0) {
        while (current !== null) {
            stack.push(current);
            current = current.left;
        }
        current = stack.pop();
        result.push(current.val);
        current = current.right;
    }

    return result;
};

時間複雜度：O(n)，需要遍歷所有節點。
空間複雜度：O(h)，使用的空間取決於樹的高度。

總結:
這道題目可以歸類為「recursion」和「stack」這兩個分類。遍歷二元樹的兩種實作方法——遞迴（recursion）和迭代（iteration）——都建議讀者學習並掌握。雖然遞迴法看似簡單，但在每次遞迴過程中，系統的 call stack 會儲存傳入參數、函數中的區域變數以及返回地址。若系統資源有限（如單晶片）且二元樹的層數過大，可能會導致stack overflow。

另一方面，迭代法使用stack來模擬遞迴過程，避免了系統 stack overflow 的風險。由於每一步操作都在迭代迴圈內進行，迭代法在調試（debug）和控制流程方面更具優勢，只是實作過程相對複雜。因此，理解並掌握這兩種方法，能讓你在不同場景下靈活選擇最適合的解法。

從這道題目開始，LeetCode 開始引入 tree（樹）相關的問題。不過，LeetCode 的設計是從簡單到複雜，這樣的進程有助於我們逐步學習並掌握 tree 相關的知識和實作方式。隨著題目難度的增加，我們可以循序漸進地加深對 tree 結構的理解，並提升解題能力。通過逐步練習，我們將能夠更加熟練地應對各種 tree 題型，為解決更具挑戰性的問題打下堅實的基礎。